
Inhaltsverzeichnis:
- Autor Sierra Becker [email protected].
- Public 2024-02-26 04:44.
- Zuletzt bearbeitet 2025-01-22 22:11.
Papierhandwerk sind nicht nur verschiedene Postkarten und Applikationen in Form von flachen Produkten. Volumetrische Modelle von Figuren sind sehr originell (Foto 1). Sie können zum Beispiel einen Polyeder aus Papier konstruieren. Sehen wir uns einige Möglichkeiten an, dies mithilfe von Diagrammen und Fotos zu tun.

Geschichte der Figuren
Die alte mathematische Wissenschaft hat ihre Wurzeln in der fernen Vergangenheit, während der Blütezeit des antiken Roms und Griechenlands. Damals war es üblich, technische Aspekte mit philosophischen zu verbinden. Daher symbolisiert nach den Lehren von Plato (einem der antiken griechischen Denker) jeder der Polyeder, die aus einer bestimmten Anzahl identischer Ebenen bestehen, ein Element. Figuren aus Dreiecken - Oktaeder, Ikosaeder und Tetraeder - sind jeweils mit Luft, Wasser und Feuer verbunden und können aufgrund der gleichen Art von Flächen, von denen jede drei Ecken hat, ineinander umgewandelt werden. Die Erde wird durch ein Hexaeder aus Quadraten symbolisiert. Und der Dodekaeder spielt dank der besonderen fünfeckigen Flächen eine dekorative Rolle und ist der Prototyp von Harmonie und Frieden.

Es ist auch bekannt, dass einer der griechischen Mathematiker, Euklid, in seiner Lehre von den "Anfängen" die Einzigartigkeit der erwähnten platonischen Körper und ihre Eigenschaft bewies, in die Kugel "einzupassen" (Foto 2). Das abgebildete Polyeder aus Papier entsteht durch F altung von zwanzig gleichschenkligen Dreiecken, die geschlossen sind. Das Diagramm zeigt deutlich ein Muster zur Herstellung einer Figur. Schauen wir uns alle Phasen der Erstellung eines Ikosaeders genauer an.
Zwanzigeder machen
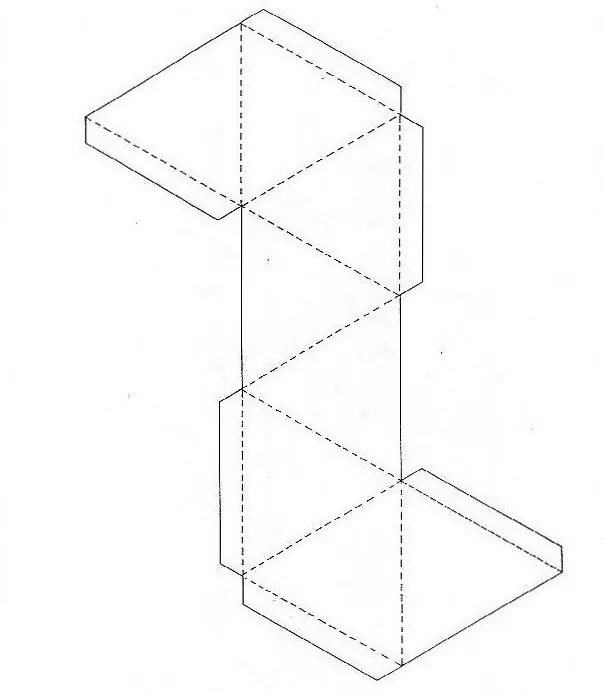
Der Ikosaeder besteht aus gleich großen, gleichschenkligen Dreiecken. Es kann einfach gef altet werden, indem die in Abbildung 2 gezeigte Entf altung verwendet wird. Nehmen Sie ein rechteckiges Blatt Papier. Zeichnen Sie darauf zwanzig Dreiecke gleicher Größe und Form und platzieren Sie sie in vier Reihen. In diesem Fall ist jede Seite des einen gleichzeitig eine Seite des anderen. Verwenden Sie die resultierende Vorlage, um ein Leerzeichen zu erstellen. Es unterscheidet sich vom Basisscan durch das Vorhandensein von Klebezugaben entlang aller Außenlinien. Nachdem Sie einen Rohling aus Papier geschnitten haben, biegen Sie ihn entlang der Linien. Bilden Sie ein Polyeder aus Papier und schließen Sie die äußersten Reihen miteinander. In diesem Fall werden die Eckpunkte der Dreiecke zu einem Punkt verbunden.

Reguläre Polyeder
Alle Figuren unterscheiden sich durch eine unterschiedliche Anzahl von Gesichtern und deren Form. Außerdem lassen sich manche Modelle aus einem einzigen Blech bauen (wie am Beispiel Ikosaederherstellung beschrieben), andere nur aus mehreren Modulen zusammenbauen. Reguläre Polyeder gelten als klassisch. Sie bestehen aus Papier und haften anDie Hauptregel der Symmetrie ist das Vorhandensein von vollständig identischen Flächen in der Vorlage. Es gibt fünf Haupttypen solcher Figuren. Die Tabelle enthält Informationen über ihre Namen, Anzahl und Formen der Gesichter:
| Name | Anzahl der Gesichter | Form jedes Gesichts |
| Tetraeder | 4 | Dreieck |
| Hexaeder | 6 | Quadrat |
| Oktaeder | 8 | Dreieck |
| Dodekaeder | 12 | Fünfeck |
| Ikosaeder | 20 | Dreieck |
Formenvielf alt

Basierend auf den fünf angegebenen Typen können Handwerker mit Geschick und Vorstellungskraft ganz einfach viele verschiedene Papiermodelle entwerfen. Ein Polyeder kann völlig anders sein als die oben beschriebenen fünf Figuren, indem er gleichzeitig aus Flächen unterschiedlicher Form gebildet wird, beispielsweise aus Quadraten und Dreiecken. So erhält man archimedische Körper. Und wenn Sie ein oder mehrere Gesichter überspringen, erh alten Sie eine offene Figur, sowohl von außen als auch von innen betrachtet. Für die Herstellung dreidimensionaler Modelle werden spezielle Muster verwendet, die aus ziemlich dichtem, gut geformtem Papier ausgeschnitten werden. Sie stellen auch spezielle Polyeder aus Papier her. Schemata solcher Produkte bietendas Vorhandensein zusätzlicher, hervorstehender Module. Sehen wir uns an, wie man am Beispiel des Dodekaeders eine sehr schöne Figur konstruieren kann (Foto 3).
Wie man aus Papier einen Polyeder mit zwölf Ecken macht: der erste Weg
Eine solche Figur wird auch Sterndodekaeder genannt. Jeder seiner Eckpunkte ist an seiner Basis ein regelmäßiges Fünfeck. Daher werden solche Papierpolyeder auf zwei Arten hergestellt. Die Schemata für die Herstellung werden sich geringfügig voneinander unterscheiden. Im ersten Fall handelt es sich um ein Einzelteil (Foto 4), wodurch das fertige Produkt aufgerollt wird. Neben den Hauptflächen enthält die Zeichnung Verbindungsteile zum Kleben, wodurch sich die Figur zu einem Ganzen schließt. Um ein Polyeder auf die zweite Art zu erstellen, müssen Sie mehrere Vorlagen separat erstellen. Betrachten wir den Arbeitsprozess genauer.

Wie erstelle ich ein Papierpolyeder: der zweite Weg
Erstelle zwei Hauptvorlagen (Bild 5):
- Zuerst. Zeichnen Sie einen Kreis auf das Blatt und teilen Sie ihn in zwei Teile. Einer wird die Grundlage für das Muster sein, den zweiten Bogen der Einfachheit halber sofort löschen. Teilen Sie das Teil in fünf gleiche Teile und begrenzen Sie alle Radien mit Quersegmenten. Das Ergebnis sind fünf identische gleichschenklige Dreiecke, die miteinander verbunden sind. Zeichnen Sie neben dem mittleren Segment genau den gleichen Halbkreis, nur spiegelverkehrt. Das resultierende Teil sieht gef altet wie zwei Kegel aus. Machen Sie solche ähnlichen Vorlagen in insgesamt sechs Stück. Zum Verklebender zweite Teil wird verwendet, der innen platziert wird.
- Sekunde. Dieses Muster ist ein fünfzackiger Stern. Führen Sie die gleichen zwölf Leerzeichen aus. Jeder der Sterne wird zu einem Polyeder mit den nach oben gebogenen Enden in die kegelförmigen Teile gelegt und an den Rändern verklebt.
Der vollständige Zusammenbau der Figur wird erreicht, indem Doppelblöcke mit zusätzlichen Papierstücken verbunden und nach innen gedreht werden. Beim Modellieren von Produkten ist es ziemlich problematisch, sie in der Größe unterschiedlich zu machen. Fertige Modelle aus Papierpolyedern lassen sich nicht so einfach vergrößern. Dazu reicht es nicht aus, nur alle Außengrenzen zu berücksichtigen. Sie müssen jede der Flächen separat skalieren. Nur so erh alten Sie eine vergrößerte Kopie des Originalmodells. Mit der zweiten Methode zur Herstellung eines Polyeders ist dies viel einfacher, da es ausreicht, die anfänglichen Rohlinge zu erhöhen, auf denen bereits die erforderliche Anzahl von Einzelteilen hergestellt wird.
Empfohlen:
Wie man einen Bommel, einen Teppich und einen Lampenschirm für eine Lampe aus Garn macht

Wenn wir uns die Arbeit professioneller Designer ansehen, sind wir oft ein wenig neidisch auf ihre Kunst und denken, dass wir zu so etwas nicht fähig sind
Wie macht man Papierpolyeder?

Papier ist ein hervorragendes Material, um interessante und ungewöhnliche Designs zu erstellen. Wenn Sie Fähigkeiten und Fertigkeiten haben, können Sie aus gewöhnlichen Albumblättern einen Schwan, ein schönes Haus, einen Weihnachtsbaum, eine Tulpe und sogar eine Schlange machen. Aber Papierpolyeder verdienen besondere Aufmerksamkeit - geometrische volumetrische Figuren
Schleife zur Entlassung aus dem Krankenhaus. Wie man mit eigenen Händen einen Bogen für einen Extrakt macht

Wenn Ihnen oder Ihren Lieben ein Kind geboren wird, beginnt nicht nur das Baby selbst, sondern auch seine Eltern ein neues Leben. Das Jungtier ist vor fremden Seitenblicken geschützt, aber gleichzeitig in bunte Windeln gekleidet. Und eine schöne Schleife für die Entladung, die Sie mit Ihren eigenen Händen hergestellt haben, wird zu einem unverzichtbaren Attribut der ersten Kindergarderobe
Wie man einen Diamanten aus Papier macht und wie man ihn im Innenraum anwendet
Die beste Heimdekoration ist eine DIY-Dekoration. Schließlich steckt man seine Seele und Kraft hinein, und das Ergebnis ist immer so unterschiedlich. Daher lohnt es sich zu lernen, wie man einen Diamanten aus Papier macht. Eine Verwendung für so ein süßes kleines Ding zu finden ist ganz einfach
Wie man aus Zapfen einen Igel macht. Do-it-yourself-Igel aus einem Kegel

Zapfen sind eine universelle Basis für Kreativität! Aus ihnen können Sie viele bezaubernde Handarbeiten herstellen. Das sind Igel und Eulen und lustige kleine Skifahrer. Alles, was Sie brauchen, ist etwas Material und ein kreativer Kopf
